موضوع نرمال بودن دادهها از مهمترین مقولات در انتخاب نوع روش آماری(پارامتری یا نا پارامتری) و آزمون فرضیات است. خیلی از محققین قبل از اجرای آزمون آماری موردنظر خود برای فرضیه ها در تردیدند که آیا توزیع دادههایشان از توزیع نرمال برخوردار هستند یا خیر. بسیار اتفاق افتاده که محققین به دلیل عدم تشخیص درست وضعیت نرمال بودن توزیع دادهها، آزمون نادرستی را اجرا کردهاند.
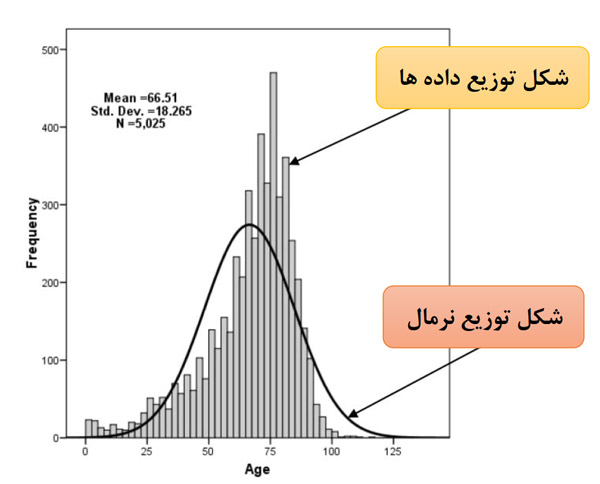
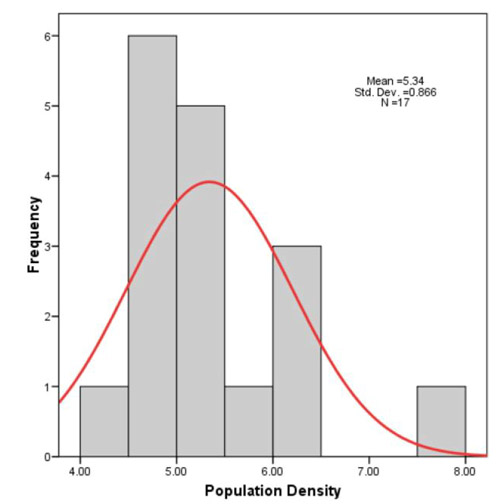
نرمال بودن دادهها یکی از پیشفرضهای مهم در آزمونهای پارامتریک است. توزیع نرمال بهصورت زنگولهای شکل است که در نگاره زیر آمده است:
فرضهای آماری در تست نرمال بودن بهصورت زیر تعریف میشوند:
- فرض صفر: دادههای نمونه از توزیع نرمال تفاوت معناداری ندارند(دادهها نرمال هستند)
- فرض مقابل: دادههای نمونه از توزیع نرمال تفاوت معناداری دارند(دادهها نرمال نیستند)
روشهای مختلفی برای بررسی نرمال بودن دادهها وجود دارد که به دو دسته کلی تقسیم میشوند:
الف) روشهای گرافیکی و شاخصهای توصیفی:
- نمودار Q-Q (چارک-چارک)
- نمودار P-P (احتمال-احتمال)
- بررسی چولگی و کشیدگی دادهها
ب) روشهای آمار استنباطی:
- آزمون کولموگروف-اسمیرنوف
- آزمون شاپیرو-ویلکس
- آزمون Jarque-Bera Test
- آزمون D’Agostino Test
شاخصهای چولگی و کشیدگی
در علم آمار چولگی یا Skewness معیاری از تقارن یا عدم تقارن تابع توزیع میباشد. برای یک توزیع کاملاً متقارن چولگی صفر و برای یک توزیع نامتقارن با کشیدگی به سمت مقادیر بالاتر چولگی مثبت و برای توزیع نامتقارن با کشیدگی به سمت مقادیر کوچکتر مقدار چولگی منفی است. کشیدگی یا kurtosis نشاندهنده ارتفاع یک توزیع است. به عبارت دیگر کشیدگی معیاری از بلندی منحنی در نقطه ماکزیمم است و مقدار کشیدگی برای توزیع نرمال برابر ۳ می باشد. کشیدگی مثبت یعنی قله توزیع موردنظر از توزیع نرمال بالاتر و کشیدگی منفی نشانه پایینتر بودن قله از توزیع نرمال است.
البته طبیعی است که روشهای گرافیکی و توصیفی بیشتر ماهیت شهودی داشته و تفاوت در تفسیر و نتیجهگیری از آنها زیاد است، بنابراین از اعتبار کمتری نسبت به روشهای آماری برخوردارند. از این رو توصیه می شود که برای درک نرمال بودن توزیع دادهها، از روشهای عددی که در ادامه آورده شده است استفاده کنیم که روشهای عینی تر و واقعی تر نسبت به روشهای گرافیکی اند.
آزمون کولموگروف-اسمیرنوف برای دادههای بیشتر از 50 عدد و آزمون شاپیرو-ویلکس برای دادههای کمتر از 50 عدد استفاده می شود علت استفاده زیاد از آزمون کولموگروف این است که این آزمون از ابتدا در نرمافزار spss وجود داشته است اما متأسفانه این آزمون به حجم نمونه حساس است برای مثال اگر حجم نمونه کم باشد بهراحتی فرض صفر را تائید میکند و در حجم نمونه زیاد، تفاوت اندک از توزیع نرمال باعث رد شدن فرض صفر می شود درصورتیکه در حجم نمونه بالا، تفاوت اندک از توزیع نرمال تأثیری بر نتایج آزمونهای پارامتریک ندارد بنابراین در منابع علمی توان آزمون شاپیرو را بیشتر از آزمون کولموگروف اسمیرنوف می دانند و استفاده از آزمون کولموگروف-اسمیرنوف را جهت تست نرمال بودن دادهها توصیه نمیکنند. هر دو آزمون در نرمافزار spss وجود دارد.
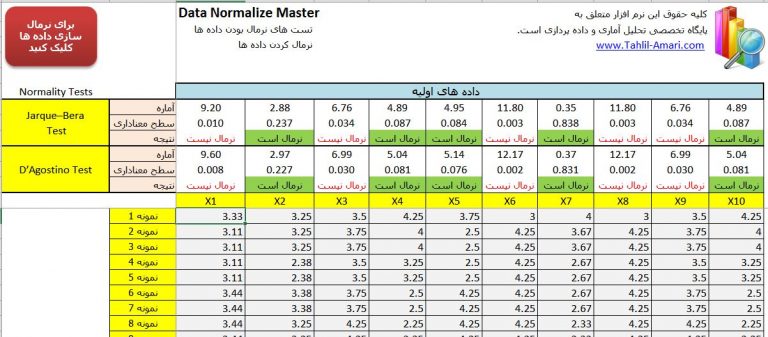
آزمونهای جدیدتر و بهتری برای تست نرمال بودن دادهها ایجاد شده است که متأسفانه در نرمافزار spss وجود ندارد. برای مثال دو آزمون Jarque-Bera و D’Agostino برای سنجش نرمال بودن دادهها از شاخصهای چولگی و کشیدگی استفاده میکنند و به حجم نمونه حساس نیستند و توان بالایی در تشخیص نرمال بودن دادهها دارند بنابراین توصیه می شود برای تست نرمال بودن از این دو آزمون استفاده شود. پایگاه تخصصی تحلیل آماری نرمافزار Data Normalize Master را طراحی کرده است که این دو تست را بر روی دادهها انجام میدهد چنانچه مشخص شد که دادهها نرمال نیستند آن وقت بر اساس الگوریتم بهبود یافته Box-Cox که در نرمافزار وجود دارد بهراحتی می توانید دادههای غیر نرمال را با فشار دادن یک دکمه به دادههای نرمال تبدیل می شود.
گاهی اوقات روش آماری معادل ناپارامتریک وجود ندارد و یا شاید تأکید شده است حتما از آزمون پارامتریک استفاده شود در این حالت نیاز است دادهها را نرمال شوند. یکی از مزایای که نرمافزار Data Normalize Master دارد این است که وقتی دادهها نرمال می شود میانگین دادهها هیچ تغییری نمیکند بنابراین نرمالسازی باعث تغییر نتایج آماری نمیشود. حتی همبستگی و تأثیرگذاری که بین متغیرها وجود دارد بعد از نرمالسازی همبستگی و تأثیرگذاری حفظ می شود بنابراین بهراحتی می توانید با نرمالسازی از همه آزمونهای پارامتریک استفاده کنید. اگر تعدادی از متغیرها نرمال و تعدادی غیر نرمال باشد توصیه می شود همه دادهها نرمالسازی شوند که ارتباط بین متغیرها تغییری نکند.
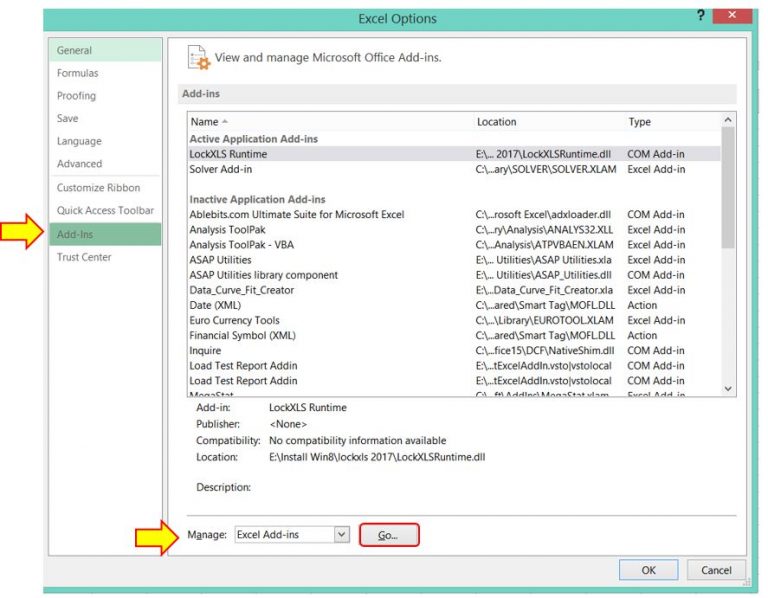
قبل از نصب نرمافزار، ابتدا نرمافزار اکسل نسخه 32 بیتی را باز کنید. از منوی File گزینه Option را انتخاب کنید. از منوی سمت چپ بر روی گزینه Add-Ins کلیک کنید. در پنجره سمت راست از منوی کرکره ای Excel Add-Ins را انتخاب کنید و بر روی دکمه Go کلیک کنید.
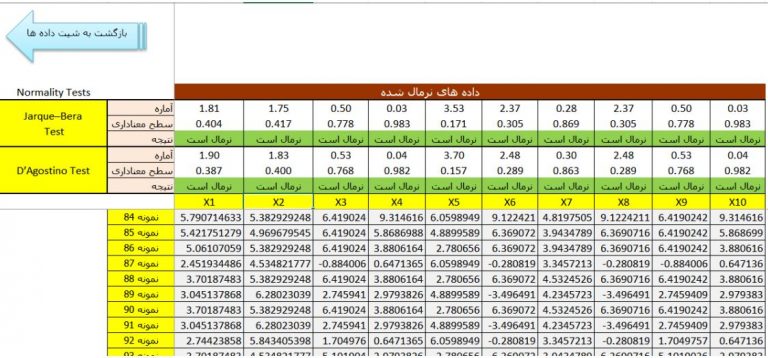
نرمافزار قادر است به طور همزمان بر روی 10 متغیر تست نرمال بودن و نرمالسازی را انجام دهد. زمانی که به دلخواه دادههای 10 متغیر را در ستون های X1تا X10 وارد کردید بطور خودکار تست نرمال بودن بر اساس دو روش آزمون Jarque-Bera و D’Agostino بالای نام متغیرها انجام میگیرد. متغیرهایی که سطح معناداری انها بیشتر از 0.05 باشد نرمال هستند و با رنگ سبز مشخص میشوند. برای انجام نرمالسازی فقط کافی است بر روی دکمه قرمز رنگ در بالای صفحه نرمافزار کلیک کنید تا دادهها نرمال شوند و نتایج بهصورت زیر می شود:
همانطور که در تصویر بالا مشاهده شده همه دادهها بهخوبی نرمال شده اند.
در هنگام استفاده از نرمافزار مطمن باشید که دادههای مفقود شده(Missing Value) نداشته باشید و یا مقادیر مفقود شده را با میانگین دادهها جایگزین کنید تا مراحل نرمالسازی دادهها بهصورت کامل انجام گیرد. پس از انجام نرمال سازی می توانید داده ها را وارد نرم افزارهای آماری کنید و از آزمون های پارامتریک استفاده کنید.